In the previous tutorial of this ongoing serie, I introduced the circle packing 2x2 algorithm.

I explained how the simple 2x2 rule, creating a new circle from 2 adjacent ones, can be iterated to produce circle packing patterns.

I also explored a first way to adapt the algorithm to create more interesting and natural patterns.

This new tutorial will build on the previous one by exploring another way to adapt the 2x2 algorithm.

It will present different ways to draw the computed circle patterns, by computing varying colors.

À first way to define colors for each computed circle is to use a similar rule as for the radius.

More precisely, we can define the color of a newly computed circle by taking into account the colors of the 2 parents and add a small variation.

A nice way to do this is to use colors described as a hue (see here the detailed description of this color format).

By defining an initial hue for the root circles, and a constant hue increment of 0.1 for each new circle, we get:

Interesting!

Of course, as for the radius in the previous tutorial, we can make this increment random, for example in the -0.2 0.2 interval, to get a centered color variation:

Nice !

This process can be extended to other parameters of the colors, in particular for the light component (see here again). We can make it synchro with the hue variation :

Or not:

This last example is interesting: varying parameters one after the other is interesting, but combining them open new kinds of algorithms that are more powerful.

So considering this point, we can go back to think about combining colors with radius variations !

A first way to synchronize radius and color when creating a new circle is just to take the same amount of variation for both quantities.

However, we must note that radius and color variations are not expressed in the same way: radius variation by a ratio between (1.2, 0.8) while color (hue) variation by an increment (-0.1,0.1).

As a consequence, to synchronize them, we first need to take a random value from a given interval (by convention (0.0,1.0)),

then map the result on the intervals of the two variables, to get the two variations.

By doing so, we get

Interesting, but somehow not easy to see the relationship between radius and color.

As a matter of fact, we are mapping increments, not quantities, and as a consequence,the relationship between them is not obvious.

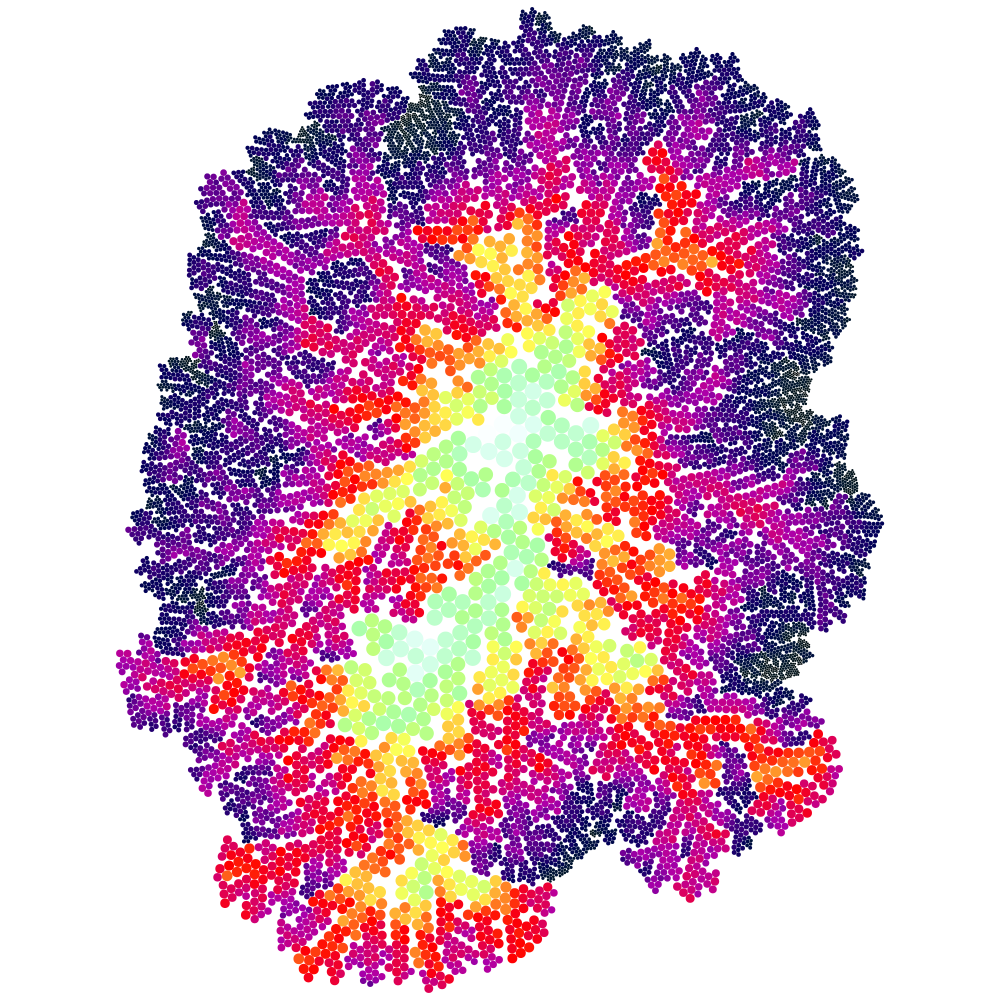
To make the relationship more noticeable, we must map the quantities themselves, for example radiuses to colors.

But to do so, to be able to compute a color, we must know the range of radiuses of the pattern.

And as such, we must abandon locality.

Every algorithm described up to now are based on local computation rules.

Attributes of a new circle are computed from increments of parents's characteristics.

As described in the previous section, if we want to map radiuses with colors, we cannot do it locally, as we must know the range of radiuses of the pattern before computing a single color.

As a consequence, we must use another type of algorithm, called non-local, whose template is the following:

By doing so, we got: